https://arxiv.org/pdf/2002.02126.pdf
Abstract
Collaborative filtering 분야에서 SOTA의 성능을 내던 GCN은 본래 graph classification을 위해 고안된 model이다.
이 논문에서는 GCN의 design 중 일부인 feature transformation / non-linear activation 가 collaborative filtering의 performance에 기여하는 바가 적고, 오히려 training을 어렵게 만듦과 동시에 performance를 떨어뜨린다는 것을 실험적으로 발견하였다.
따라서 불필요한 design들은 모두 버리고 GCN에서 가장 필수적인 요소인 'neighborhood aggregation'만을 남긴 model인 'LightGCN' model을 새롭게 제시한다.
LightGCN은 user-item graph에서 embedding들을 linear하게 prapagating 함으로써 user, item embedding들을 학습하고, 마지막 embedding에서 모든 layer에서 학습했던 embedding들을 weighted sum한다.
이렇게 간단하고 linear하고, 깔끔한 model은 훈련과정과 구현에 있어 훨씬 쉽다.
2. Preliminaries
2.1 NGCF Brief
첫번째 step에서 각각의 user / item은 ID embedding으로 이루어져 있다.
NGCF에서는 다음과 같이 user-item interaction graph에 영향을 미친다.

L layer에 propagating 함으로써, NGCF는 L+1개의 embeddings들을 가지고


최종 embedding 과정에서 prediction score를 구하기 위해 user / item embedding vector를 inner product를 이용하여 concat 시킨다.
NGCF는 standard GCN을 따르기 때문에 non-linear activation function과 feature transformation W1, W2를 가지고 있다.
하지만 여기서 위 operation들은 collaborative filtering에 필요 없음을 주장한다.
Semi-supervised node classification task에서는 각각의 node가 rich semantic feature들을 input에서부터 가지고 있기 때문에 feature learning에 효율적으로 사용할 수 있지만, collaborative filtering에서는 input이 ID embedding이기 때문에 concrete semantics들을 가지고 있지 않다. 이 경우에 여러 개의 non-linear transformation들은 better feature들을 학습하는데 영향을 끼치지 못하고, 심지어는 훈련시에 difficulties만 증가시키게 된다.
2.2 Empirical Explorations on NGCF
여기서 non-linear activation과 feature transformation가 NGCF에 어떤 영향을 끼치는지 알아보기 위해 NGCF 저자의 코드를 이용하여 ablation study를 진행했다.

NGCF-f를 확인해보면 기존 NGCF보다 더 좋은 성능을 내는 것을 확인할 수 있다.
반면에 NGCF-n을 확인해보면 오히려 기존보다 좋지 않은 성능을 내는 것을 확인할 수 있다.
그런데 여기서 non-linear activation과 feature transformation을 모두 제거한 NGCF-fn의 경우 정확도가 매우 개선된 것을 확인할 수 있다.
이러한 결과를 통해 논문에서는
(1) feature transformation을 추가하는 것은 NGCF에 좋지 않은 영향을 미친다.
-> NGCF와 NGCF-n 에서 f를 제거하였을 때 perfomance가 크게 증가하였기 때문
(2) NGCF에 feature transformation이 있는 경우 non-linear activation이 추가할 때 아주 약간 성능이 향상하지만, 없는 경우에는 오히려 negative effect가 생긴다.
(3) 전체적으로 보았을 때, feature transformation과 non-linear activation은 negative effect를 유발하고, 반대로 동시에 제거하는 경우에는 성능이 크게 향상된다.
추가적으로 training loss가 작은 경우에는 대체로 좋은 accuracy를 내는 것을 확인하였고, NGCF와 NGCF-f를 비교하였을 때 training loss는 비슷하지만 NGCF-f가 더 좋은 성능을 내는 것을 볼 때, NGCF 성능 저하의 원인은 overfitting 보다는 training difficulty임을 추론할 수 있다.
따라서 불필요한 operation을 추가하는 것은 training difficulty를 증가시키고, 결국 model을 degrade 시킬 수 있음을 알 수 있다.
3. Method
3.1 LightGCN
3.1.1 Light Graph Convolution

lightGCN에서의 Graph Convolution operation을 살펴보면 다음과 같다.
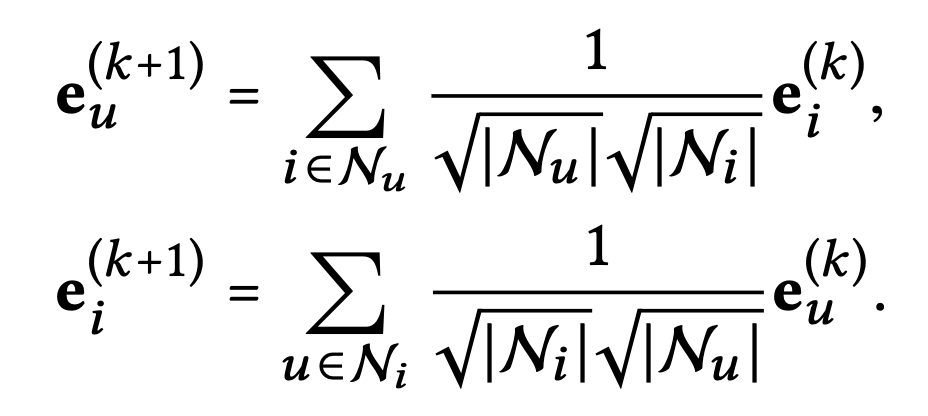
여기서는 sum aggregator를 간단하게 하고, feature transformation과 nonlinear activation은 제거하였다.
3.1.2 Layer Combination and Model Prediction
LightGCN에서 유일하게 trainable한 parameter는 0-th layer의 embedding이다.
higher layer에서의 embedding은 위 공식을 이용한 propagation으로만 구할 수 있고, 최종 embedding vector는 아래와 같이 구할 수 있다.

여기서 alpha_k는 k-th embadding layer의 중요도를 의미하는 가중치이다.
alpha_k를 1/(K+1) 로 하는 경우 일반적으로 가장 좋은 성능을 낸다.
이는 모든 layer에서의 embedding을 combine하여 최종 embedding을 얻는 것을 의미하는데, 이유는 아래와 같다.
(1) layer가 많아질수록 embedding들은 over-smoothed되기 때문에, 단순히 마지막 layer만을 이용하여 최종 embedding을 구하는 것은 문제가 있다.
(2) 각각의 layer들은 서로 다른 sematnics들을 가지고 있다. 예를 들어, 첫번째 layer는 interaction을 가지고 있는 user, item들을 smooth하게 만들고, 두번째 layer에서는 서로 겹치는 items(users)들을 가지고 있는 users(items)들을 smooth한다. higher layer에서는 고차의 연결 구조에 대한 정보를 의미한다. 따라서 이들을 결합하면 더 많은 것을 포함할 수 있는 representation이 만들어진다.
(3) weighted sum을 이용하여 서로 다른 layer들의 embedding을 결합하는 것은 self-connection을 가지고 있는 효과를 낼 수 있기 때문에, 중요한 trick으로 이용될 수 있다.
마지막 최종 score는 다음과 같은 inner product로 구할 수 있다.

3.1.3 Matrix Form
user-item interaction matrix를 R(R_ui : u가 item i와 interact한다면 1, 아니면 0)이라 한다면 user-item graph의 adjacency matrix는 다음과 같이 구할 수 있다.

또한 0-th embedding matrix를 E0라 한다면, LGC의 matrix equivalent form을 다음과 같이 얻을 수 있다.

D는 (M + N) x (M + N)의 대각행렬로, degree matrix를 의미한다.
최종 embedding matrix는 다음과 같이 얻을 수 있다.

매 layer에 가중치를 A`를 곱한 값을 combine하여 최종 embedding을 구할 수 있고, A' = D^(-1/2) A D^(-1/2)를 의미한다.
식을 보면 초기 embedding 값인 E0는 고정되어 있고, layer가 깊어질수록 가중치 A`만 제곱해주기 때문에 연산의 효율성이 증가하는 것을 확인할 수 있다.
3.2 Model Analysis
저자는 LightGCN의 simple design에 대한 합리성을 증명하기 위해 세가지 측면에서 논의하였다.
3.2.1 Relation with SGCN
먼저 LightGCN이 self-connection 과정이 없어도, 있는 것과 같은 효과를 낼 수 있다는 점을 확인한다.
SGCN에서는 non-linearity를 제거하여 GCN을 간단히 하였다.
self-connection은 인접 행렬 A에서 Identity matrix를 더함으로서 나타낼 수 있는데, SGCN에서는 다음과 같이 embedding 을 정의 할 수 있다.

이때 (D+I)^(-1/2) term은 단순히 re-scale embedding을 의미하기 때문에 고려하지 않는다고 하면
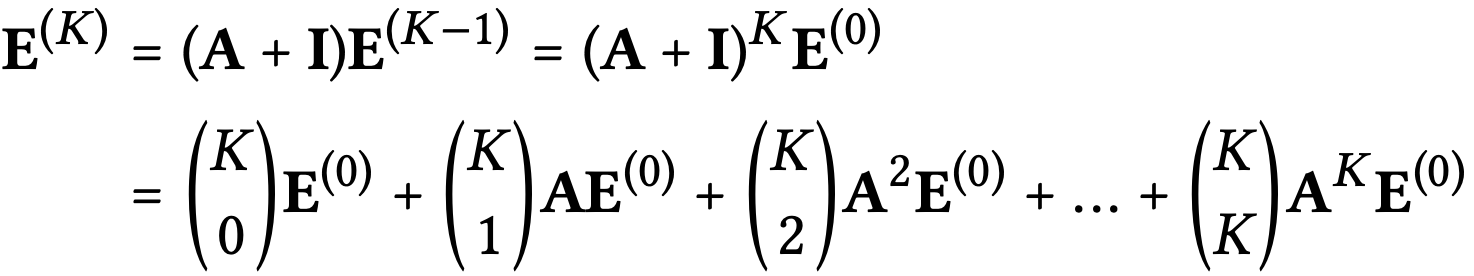
K번째 embedding은 (A+I)를 K번 제곱하여 구할 수 있고, 이항정리를 이용해 위와같이 전개할 수 있다.

식을 확인해보면 위에서 언급한 weighted sum of the embeddings propagated at each LGC layer와 같은 형태를 보이는 것을 확인할 수 있다.
3.2.2 Relation with APPNP
APPNP에서는 trainable Weight W를 0번째 층에만 넣고, 그 이후의 layer에서는 W를 없애 training을 단순화 하였다.
이 방법을 통해 layer의 개수가 증가하였을 때 over-smoothing되는 현상을 막을 수 있고, 실험을 통해 accuracy가 감소하지 않는다는 점을 확인하였다.
요약하자면 over-smoothing의 위험 없이 long range propagation이 가능한 모델을 제안하였다.
LightGCN에서는 마지막 layer에서의 over-smoothed를 막기 위해 weighted sum을 사용하였다.
over-smoothed는 최종 layer로 올라갈 수록 node들이 가까워지기 때문에 embedding 값이 유사해져 performance를 저하시키는 요인이 된다.
이 때문에 k-th embedding을 구하기 위해서 초기 embedding인 E0를 더해 over-smoothing 되는 것을 막아준다.


3.2.3 Second-Order Embedding Smoothness
user(item)과 연결된 item(user)의 second-order layer를 분석해 embedding smoothness를 구할 수 있다.
아래 식은 user의 입장에서 먼저 작성


위 식을 이용하여 second-order에 있는 user v가 user u에 미치는 영향력은 다음과 같이 해석할 수 있다.
1) 같이 공유하는 item이 많을 수록 영향력은 더욱 커진다.
-> 위 식에서 i 값이 커지기 때문에 많은 항이 더해짐
2) 같이 공유하는 item의 popularity가 작을수록 영향력은 더욱 커진다.
-> popularity가 크면 해당 item을 많은 user들이 가지고 있다는 의미
-> popularity가 작으면 Ni 값이 작다는 의미이고, 1/|Ni|의 값은 커지기 때문에
3) v가 less active할 수록 영향력은 커진다.
->v가 less active하다면 Nv값도 작아짐
또한 LightGCN은 symmetric formulation이기 때문에 item side에서도 비슷한 분석을 진행할 수 있다.
3.3 Model Training
LightGCN의 trainable parameter는 유일하게 0-th layer의 embedding뿐이다. i.e. Θ ={E0}
따라서 model의 complexity가 standard matrix factorization과 같다.
Loss는 BPR loss를 사용하여 관측된 entry에 대한 prediction 값이 관측되지 않은 entry의 prediction보다 커지도록 하는 pairwise loss를 사용하였다.

λ는 L2 regularization length를 조절하는 역할을 한다.
또한 여기서는 GCN과 NGCF에서 보편적으로 사용되는 dropout 기법에 대해 논하지 않는데, 이는 LightGCN에서는 L2 regularization를 사용하면서, feature transformation weight metrices를 사용하지 않기 때문에 충분히 overfitting을 막을 수 있기 때문이다.
6. Conclusion
이 논문에서는 크게 두가지로 구성된 LightGCN을 제시한다.
1) Light graph convolution
featrue transformation과 nonlinear activation 구조를 제거하면서 training difficulty를 줄인다.
2) Layer combination
final embedding 과정을 weighted sum으로 구하게 되면서 self-connection의 효과를 낼 뿐만 아니라 oversmoothing을 control 한다.
Simple하다는 장점을 가진 LightGCN은 training이 더 쉽고, 더 좋은 generalization ability와 더욱 effective하다는 것을 실험을 통해 확인할 수 있다.




댓글