https://arxiv.org/pdf/1205.2618.pdf
코드 구현
GitHub - 327aem/bpr: BPR: Bayesian Personalized Ranking from Implicit Feedback torch implementation
BPR: Bayesian Personalized Ranking from Implicit Feedback torch implementation - GitHub - 327aem/bpr: BPR: Bayesian Personalized Ranking from Implicit Feedback torch implementation
github.com
Abstract
지금까지의 추천 시스템 모델 중에서 implicit feedback을 다루는 모델은 'matrix factorization(MF)'나 'adaptive K-Nearest-neighbor (kNN)' 모델이 있다.
이 모델들은 personalized ranking을 위해 고안되었지만, 직접적으로 ranking을 optimize 하지 않는다.
이 논문에서는 Bayesian analysis 에서의 Maximum posterior estimator 를 이용한 BPR-Opt criterion optimization을 제시한다.
해당 criterion을 적용한 MF / kNN 기법에서 기존 learning techniques보다 훨씬 더 좋은 성능을 내었다.
Introduction
추천 시스템에서는 sale이나 view를 직접적으로 증가시킬 수 있는 content provider나 customer를 중점으로 personalization 할 수 있지만, 이 논문에서는 item recommandation에 초점을 맞추었다.
최근 user가 제공하는 'rating'과 같은 explicit feedback에 대한 연구가 많지만, 그럼에도 불구하고 real-world scenario에서는 explict보단 implicit feedback이 많다. Monitoring clicks, view times, purchase 와 같은 정보들은 자동으로 수집되고 해당 사이트의 log files에 저장 되기 때문에 데이터를 모으기도 쉬운 반면, user들은 자신들의 선호를 직접적으로 표현하는 경우가 많이 없기 때문이다.
이 논문의 contribution은 다음과 같다.
1. Maximum posterior estimator를 이용하는 BPR-Opt를 제시한다.
2. BPR-Opt를 maximizing 하기 위해 bootstrap sampling을 이용한 stochastic gradient descent의 방법으로 'LEARN BPR'이라는 generic learning algorithm을 제시한다. 해당 방법이 BPR-Opt에서는 standard GD보다 뛰어나다고 한다.
3. 'Learn BPR' 방법을 최근 Recommender system의 SOTA model에 어떻게 적용하는지 보여준다.
4. 위와 같은 방법이 personalized ranking 방법에서 다른 learning method보다 더욱 뛰어난 성능을 보여준다.
3. Personalized Ranking
이 논문에서는 '과거에 구매한 이력'과 같은 implicit 정보들로 ranking을 추론하는 scenario를 조사하는 것을 목표로 하였다.
Implicit feedback은 크게 세가지로 나눌 수 있는데
- Positive observations (user가 구매한 item)
- Negative observations are mixture of ..
1) Negative feedback (user가 사고 싶지 않은 item)
2) Missing values (user가 미래에 사고 싶어 질 수 있는 item)
3.1 Formalization
U : set of all users
I : set of all items
라고 할 때
item에 대한 선호도를 >u라는 기호로 나타낼 수 있다.
그리고 다음과 같은 성질을 만족한다.

3.2 Analysis of the problem setting
Implicit feedback은 positive feedback일 때만 관측 가능하고, 남아있는 negative and missing value들을 어떻게 다루어야 할지에 대한 논의가 있다.
가장 보편적인 approach는 해당 value들을 모두 무시하도록 설계되는데, 이는 나중에 user가 사용할지도 모르는 item들을 모두 Negative(user가 사용하지 않을 item)으로 생각하여 무시해버리기 때문에 learning에 문제가 생긴다는 단점이 존재하였다.
(positive = 1 / negative + missing = 0)
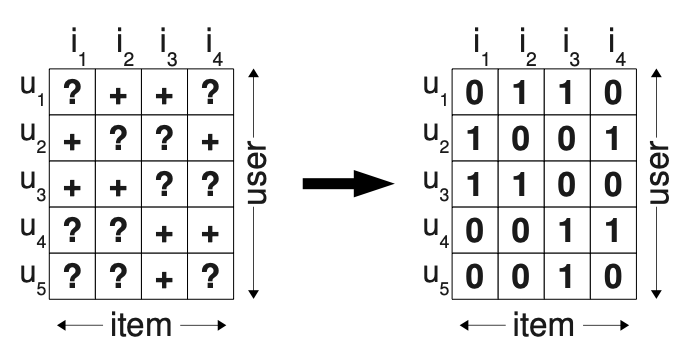
그래서 이 논문에서는 item들에 대한 scoring 대신 training data에서 item pairs들을 만들어 ranking item pair들을 optimize 하는 방법을 제안한다.
해당 pair들을 만들기전 몇 가지 규칙을 정하였는데
1) 관측된 item들은 항상 관측되지 않은 item보다 선호도가 높다.
2) 관측된 item들 사이의 선호도는 비교할 수 없다. (어떤 item이 더 선호되는지 파악할 수 없음)
3) 관측되지 않은 item들 사이의 선호도도 비교할 수 없다.

위 방법을 사용하였을 때 두가지의 장점이 있다고 하는데,
- Missing value에 대한 정보가 간접적으로 주어져 미래에 rank가 학습될 수 있음 (0이 아니기 때문에 나중에는 학습되어질 parameter가 됨)
- The training data is created for the actual objective of ranking, i.e. the observed subset DS of >u is used as training data. (추후 수정)
4. Bayesian Personalized Ranking
4.1 BPR Optimization Criterion

>u : user u가 잠재적으로 선호하는 선호도 순서
Θ : model class parameter (여기선 item, user latent vector)
BPR Opt의 목표는 >u의 정보가 주어졌을 때 위와 같은 확률을 최대화 할 수 있는(선호도 순서를 가장 잘 표현할 수 있는) Θ(item, user vector)를 찾는 것에 주목한다.
이제 우변으로 넘어가서

p(>u|Θ) 부분을 likelihood라고 부르고 선호도 >u에 대한 set을 Ds로 정의한다면
선호도에 대한 정보는 i >u j 또는 j >u i 두가지 경우만 존재하므로 >u에 대한 분포를 베르누이 분포로 나타낼 수 있다.
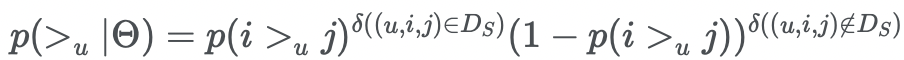
또한 p(i >u j)에 대한 값은 해당 score는 MF나 kNN model을 이용하여 x_uij의 score 값을 구한 후, 이를 sigmoid 함수에 넣어 확률을 구할 수 있다.

p(Θ)의 경우 0을 평균으로 하고 ∑Θ를 variance-covariance로 하는 분포를 따르도록 한다.
이때 unknown hyperparameter를 줄일 수 있도록 ∑Θ를 λΘI로 치환하여 풀 수 있다.
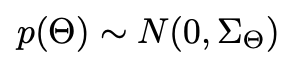
따라서 BPR-Opt를 정리해보자면
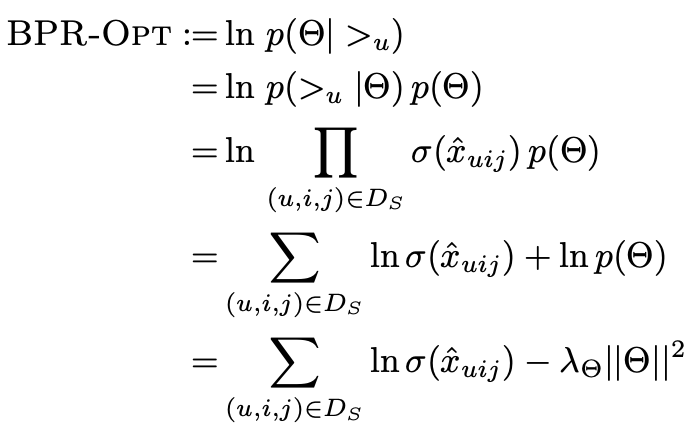
해당 확률을 최대화 할 Θ를 찾도록 하는 generic optimization criterion를 정의할 수 있다.
4.2 BPR Learning Algorithm
위에서 제시한 optimization criterion은 미분가능하므로 gradient descent based algorithm이 최적의 방법일 것이다.
하지만 standard GD 방법은 우리의 problem을 명확하게 다룰 수 없기 때문에 'LEARN BPR'을 새롭게 제시한다.
해당 방법은 stochastic GD 방법과 bootstrap sampling 기법을 적용하였다.
먼저 BPR-Opt의 gradient는
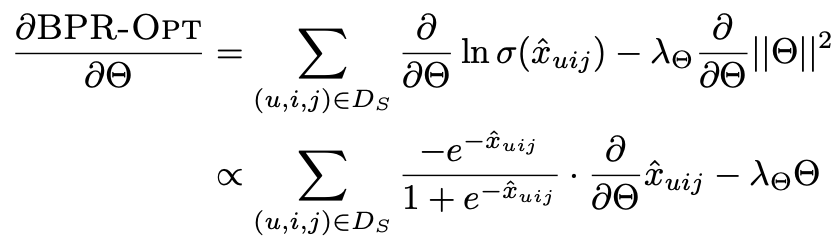
와 같기 때문에

이때 Gradient Descent 방법에는 Full / Stochastic 두가지 방법이 있다.
1) Full GD
모든 training data에 대한 gradient를 계산하고, 해당 값과 learning rate 'alpha'를 이용하여 parameter를 update하는 방법으로
다음의 식과 같다.

이 방법은 보편적으로 'correct'한 방향으로 이끌지만, 많은 양을 계산한 후 update를 진행하므로 수렴이 늦다는 단점이 있다. 또한 Ds로부터 O(|S||I|) training triples를 훈련 데이터로 사용하기 때문에 매 step마다 이를 계산하여 update하는 것을 거의 불가능하다.
또한 이는 training pairs 사이의 skewness를 유발하여 poor convergence를 일으킨다.
예를 들어 item i가 대부분의 user들에게서 positive 하다고 가정할 경우, loss를 구할 때 대부분의 term에서 item i와 다른 negative j 사이의 관계를 이용하게 되므로 i가 gradient에 지배적인 영향을 끼치게 될 것이다.
이러한 문제는 결국 learning rate를 낮게 만들어 해결하여야 하는데, 이는 loss를 매우 늦게 수렴하게 만든다.
2) stochastic GD

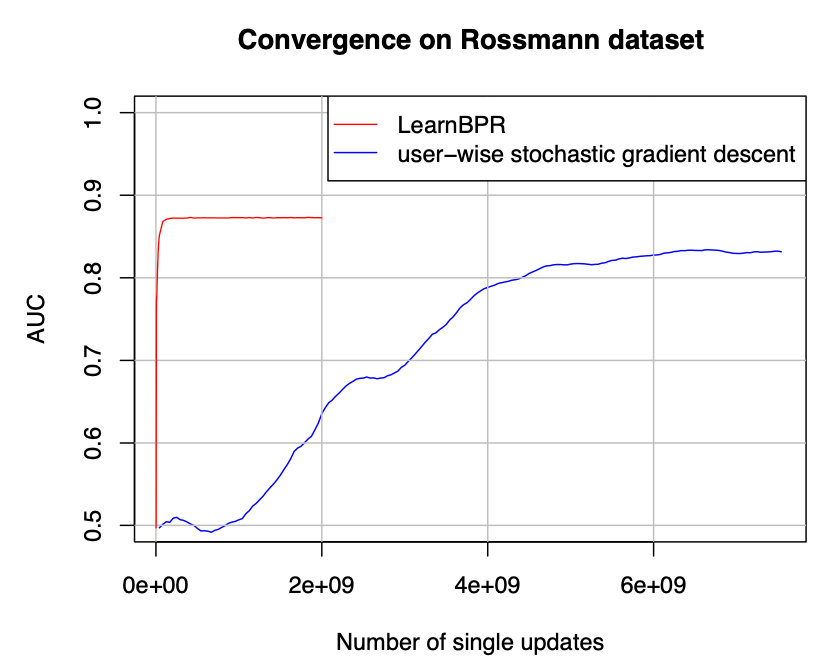
SGD 방법은 위에서 언급한 skew problem에서 대부분 좋은 approach이지만, 훈련에 들어가는 training pair의 순서가 매우 critical하다.
만약 item-wise or user-wise 하게 훈련에 들어가게 되는 경우, 같은 user-item pair가 연속적으로 훈련될 수 있기 때문에 poor convergence를 보일 수 있다.
이러한 문제를 해결하기 위해 random하게 triples를 뽑아내어 훈련에 사용할 수 있도록 한다. 또한 bootstrap sampling을 이용할 수 있도록 하여 any step에도 훈련을 종료할 수 있도록 한다.
4.3 Learning models with BPR

먼저 u,i,j에 대한 score를 x_ui - x_uj로 decomposition 할 수 있다.
이는 user u가 i를 선호한다고 한 score에서 u가 j를 선호한다고 한 score를 뺀 값으로 분해할 수 있는데, 잘 추정된 score일 수록 해당 값이 1 값을 가지게 된다.
4.3.1 Matrix Factorization
score x_ui를 예측하는 것은 결국 matrix X : U x I 를 추정하는 것으로 볼 수 있다.
target matrix X를 W : |U| x k와 H : |I| x k 두개의 low-rank matrices의 matrix product로 근사할 수 있고 다음과 같은 식으로 나타낼 수 있다.
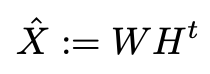
이때 k는 dimensionality / rank of the approximation으로 나타낼 수 있다.
각각의 W 행렬의 row w는 user u를 나타낼 수 있는 feature vector로 볼 수 있고, H 행렬의 row h는 item i를 나타낼 수 있는 feature vector로 볼 수 있다.
따라서 score를 다음과 같이 나타낼 수 있다.
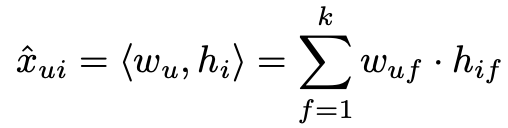
일반적으로 SVD를 이용하여 근사치를 구할 수 있지만, 머신러닝 task에서 overfitiing을 발생시키기 때문에 MF가 주로 사용된다.
또한 해당 task가 ranking task(item 사이의 선호도 순위를 파악하는 task)인 경우에는 위에서 제시된 BPR-Opt를 optimize 하는 것이 더 좋다고 한다.(Learn BPR 기법 사용)
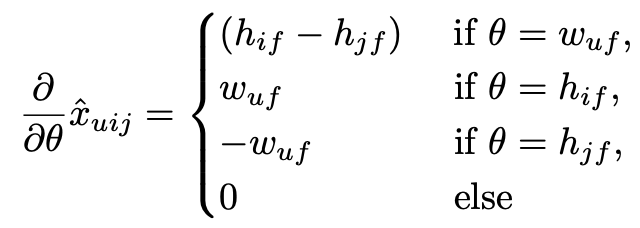
4.3.2 Adaptive k-Nearest-Neighbor
main idea는 user u와 item i에 대한 예측은 해당 item i와 이전에 발견된 것 item들인 I+ 사이의 similarity와 관련이 있다.
따라서 score x_ui는 이전에 발견되었던 item들과의 비교를 통해 알아낼 수 있다.

where C : I X I (item사이의 상관관계를 가진 대칭행렬) , parameter : C
이때 유사도는 코사인 유사도 기법을 이용하여 구한다.
kNN에서도 마찬가지로 ranking task의 경우 BPR optimization과 LearnBPR algorithm을 적용할 수 있다.

7. Conclusion
이 논문에서는 personalized ranking task에 관한 generic optimization criterion과 learning algorithm을 제시하였다.
해당 기법은 기존 model의 learning 기법 중에서 outperformance를 보여주었는데, 이를 통해 prediction quality는 model 뿐만 아니라 optimization criterion과도 크게 관련이 있다는 것을 확인할 수 있었다.
이론적, 실험적으로 확인해 보았을 때 BPR optimization 기법은 personalized ranking task에서 명확한 선택일 것이라고 말한다.




댓글