https://arxiv.org/pdf/1708.05031.pdf
Abstract
최근 몇년동안 DNN 기법은 여러 분야에서 큰 성공을 거두었지만 추천 시스템에서는 많이 사용되지 않았다.
사용되더라도 model auxiliary information에서만 사용되었고, user와 item feature의 상관관계를 조사할 때는 여전히 MF 후 inner product를 이용해 score를 sorting하는 과정을 거치고 있었다.
이러한 inner product를 대체하기 위해, 해당 논문에서는 NCF라는 새로운 framework를 제시하였다.
또한 이러한 non-linearity 성질을 충분히 이용하기 위해 multi-layer perception 기법을 제안하였다.
위 방법들은 sota의 성능을 보였고, 실험적으로 보았을 때 더 깊은 network 일수록 더 좋은 성능을 냈다고 한다.
3. Neural Collaborative Filtering
3.1 General Framework

해당 network는 user-item 사이의 interaction을 modeling하기 위해 multi-layer representation을 채택하였다.
가장 아래에 있는 input layer는 user와 item의 정보를 묘사하고 있는 feature vector이다.
해당 vector는 one-hot encoding 기법을 이용해 sparse vector로 만든다.
두 벡터를 동시에 사용하는 방법은 content feature가 user와 item을 표현하도록 사용됨으로서 cold-start problem을 쉽게 다룰 수 있도록 한다.
input layer 바로 위에 있는 layer는 embedding layer이다.
Fully connected layer를 사용해서 sparse 벡터를 dense 벡터로 변환하는 과정을 거친다.
이러한 과정으로 얻은 embedding vector는 latent factor model의 context에 있는 latent vector로 생각할 수 있다.
이 embedding vector를 NCF layer에 넣어 latent vector를 prediction score로 mapping한다.
마지막 layer에서는 최종 score를 예측하게 되는데, 예측 score인 y^ui와 target score인 y_ui 사이의 pointwise loss를 최소화 하도록 training이 진행된다.
또한 BPR이나 margin-based loss 를 사용하여 pairwise learning으로 train 할 수도 있다.
이제 NCF model를 수식으로 정리하면 아래와 같이 정리할 수 있다.
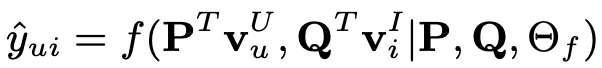
P,Q는 user와 item의 latent factor matrix를 의미하고, Θf 는 interaction function f의 parameter를 의미한다.
이때 f는 multi-layer neural network로 정의할 수 있기 때문에 f는 다음과 같이 정의할 수 있다.

φ는 mapping function, X는 layer의 개수를 의미한다.
3.1.1 Learning NCF
model의 parameter를 학습하기 위해 pointwise method를 사용하였다.

Y는 관측된 interaction들을, Y-는 관측되지 않은 interaction들을 의미한다.
w는 training시의 weight를 의미하는 하이퍼파라미터이다.
또한 현재 y의 값은 0, 1로 binalize되어 있기 때문에 probabilistic explanation을 위해 output layer에서는 logistic / probit function과 같은 probabilistic function을 activation function으로서 사용한다.


위 목적 함수를 이용하여 최소화 할 수 있도록 NCF model에 적용한다.
3.2 Generalized Matrix Factorization (GMF)
이 part에서는 MF 가 NCF framework의 special case라는 점을 보여준다.
먼저 NCF는 다음과 같은 수식으로 나타낼 수 있는데
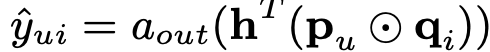
⊙는 element-wise product를 의미하고, a_out는 activation function, h는 output layer의 edge weight를 의미한다.
이때 a_out을 identity function으로, h를 1 값을 가지는 vector( [1,1,....,1] )로 설정 하면 MF와 동일하게 된다.
GMF는 a_out을 sigmoid function으로, h를 'log loss'로 학습될 수 있도록 하여 non-uniform 한 값으로 일반화 한 것을 의미하고
a_out을 non-linear하게 두면 linear MF model 보다 더욱 잘 표현할 수 있도록 하고, h를 non-uniform 값으로 설정하면 내적하는 과정에서 각각의 term에 다른 가중치를 두어 중요도를 조절할 수 있게 된다.
3.3 Multi-Layer Perception (MLP)
NCF 기법은 user / item 두개의 pathway를 서로 결합하여 훈련을 진행하는데, 이는 multi-modal deep learning work에 널리 사용되고 있다.
하지만 MF를 이용하여 단순히 두 vector를 concat하는 것은 둘 사이의 interaction을 충분히 반영할 수 없기 때문에, hidden layer를 추가하여 layer마다 user 와 item latent feature 사이의 interaction을 학습할 수 있도록 설계한다.
이 방법은 단순히 element-wise product를 이용한 GMF보다 model에 large level of flexibility와 non-linearity를 부여할 수 있다.
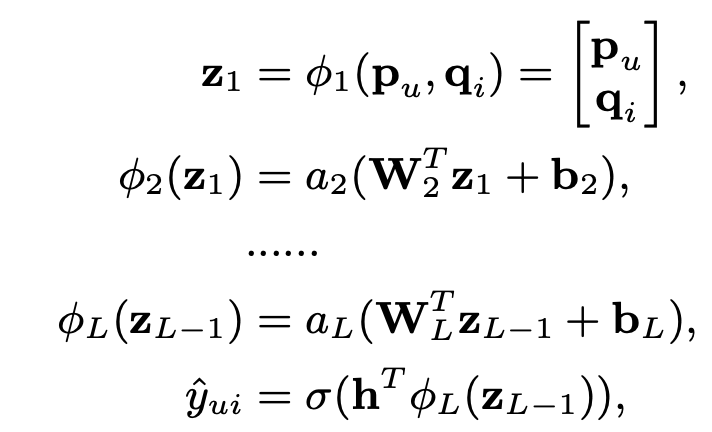
3.4 Fusion of GMF and MLP
GMF에서는 linear kernel을 적용하여 latent feature interaction들을 model 할 수 있도록 하고, MLP에서는 non-linear kernel을 적용하여 data로부터 interaction function이 학습될 수 있도록 하였다.
결국 이 둘을 합치게 되면 복잡한 user-item interaction에서 서로가 서로를 강화시키며 model을 만들어 낼 수 있다.
첫번째 방법으로는 직관적으로 GMF와 MLP 둘다 같은 embedding layer를 사용하는 것이다. 이는 서로가 비슷한 spirit을 공유할 수있다.
하지만 이는 fused model로서의 performance를 제한하는 결과를 낳을 수 있다.
두 dataset 각각의 optimal한 embedding size가 존재할 수 있는데, embedding layer를 공유하는 경우 같은 embedding size를 사용하여야 하므로 optimal한 ensemble을 얻는데 실패할 수 있다.
더욱 flexible한 model을 얻기 위해, GMF와 MLP가 분리된 embedding을 학습할 수 있도록 하고, 마지막 hidden layer에서 두 model을 concat할 수 있도록 한다.
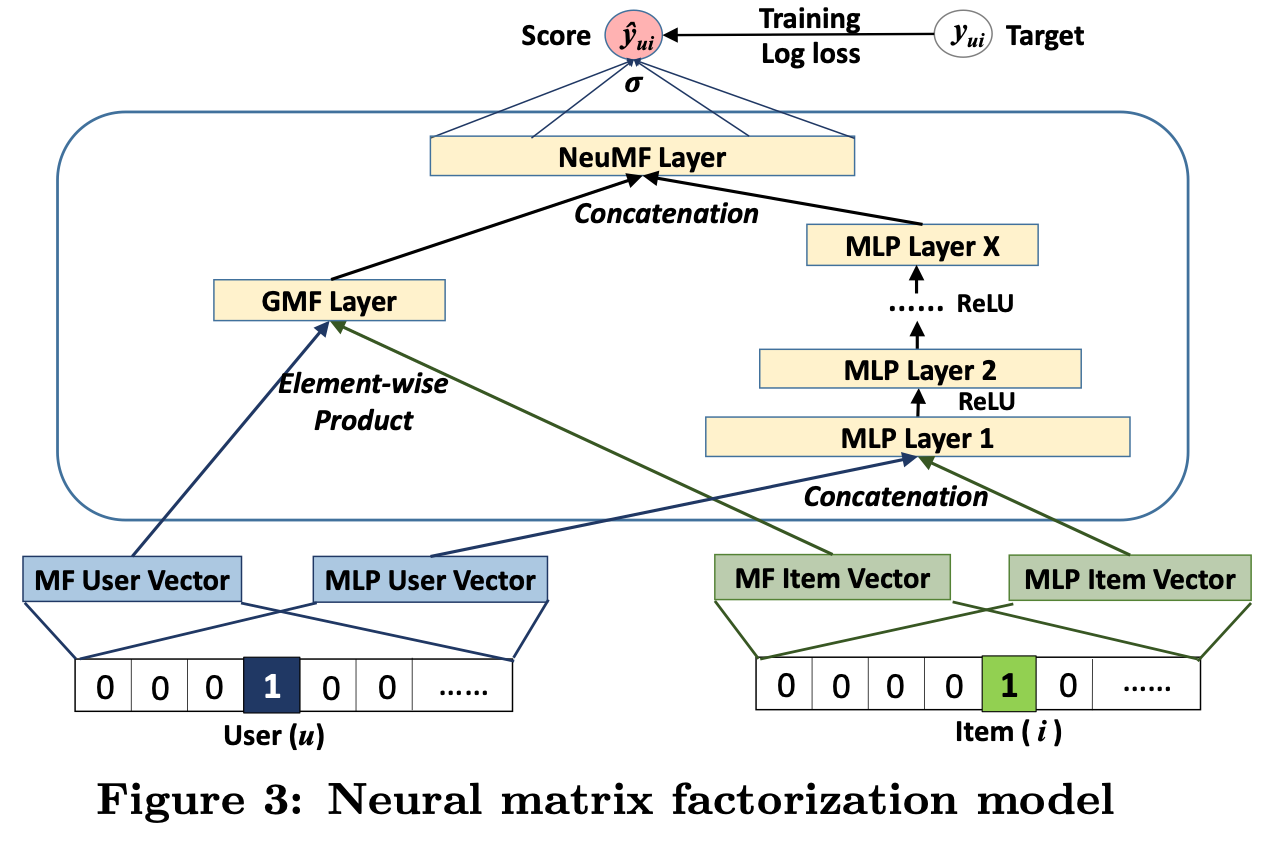
이는 아래와 같이 formulation할 수 있다.

위 모델은 MF의 linearity와 DNN의 non-linearity를 결합한 model 로서 "NeuMF(Neural Matrix Factorization)"으로 명명하기로 한다.
3.4.1 Pre-training
학습시 초기값을 설정하는 것은 굉장히 중요하므로 NeuMF model의 경우 GMF와 MLP model을 먼저 수렴할 때까지 학습한 후 NeuMF model에 적용한다.
6. Conclusion
이 논문은 기존 MF method를 사용함으로서 발생하는 linearity의 한계를 DNN을 도입함으로서 해결하려 하였다.
또한 두 model을 결합함으로서 서로를 보완할 수 있도록 하였다.




댓글