본 글은
SLAM 한국어 강의
https://www.youtube.com/c/SLAMKR
Cyrill Stachniss 교수님
https://www.youtube.com/playlist?list=PLgnQpQtFTOGQrZ4O5QzbIHgl3b1JHimN_
강의를 듣고 개인적으로 정리한 글입니다.
Introduction
Pose Graph에서는 Least Squares 방법을 사용하여 error를 최소화 한다.
일반적으로 사용되는 General Least Squares는
Squared error값의 합을 최소화하는 것으로 Gaussian 분포를 edge가 따를 때에 사용 가능하다.
Problems of G.L.S(General Least Squares)
1. Gaussian distribution
Data Association에서의 모호함 때문에, Gaussian 분포가 제데로 사용되기 어렵다.
Data Association에서 mistake가 발생하게 되면, probability mass가 튀는 현상이 발생하게 된다.
=>Standard Least Squares에서는 outlier가 존재하지 않음을 가정하였지만 Real-world에서는 outlier와 ambiguities가 발생할 수 밖에 없는 구조이기 때문에 이를 다룰 수 있어야 한다.

2. Optimization is sensitive to outliers
만약 어떠한 data point가 추정치로부터 멀리 떨어져 있는 경우에 error의 값이 제곱으로 커지게 되므로 확률이 크게 튀게 된다.
When outliers occur?
- 같은 물체가 반복해서 나타날 때
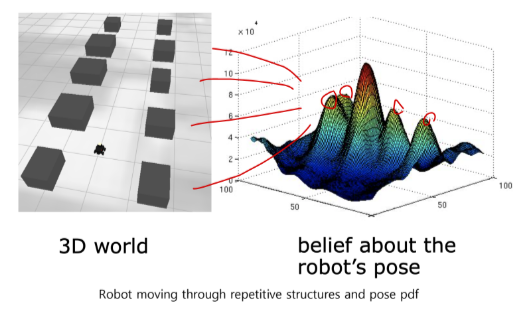
Outlier가 발생한 경우에는 어떻게 되는가?
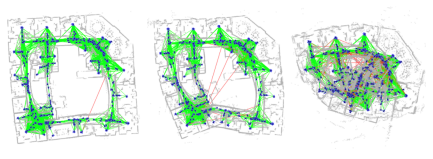
오른쪽으로 갈수록 Outlier(빨간색 선)이 증가하는 것을 확인할 수 있는데, map이 오른쪽으로 갈 수록 일그러지는 것을 확인할 수 있다. => 제대로 된 mapping이 이루어지지 않는다.
How to deal with this problem?
1. Max Mixture or Dealing with multiple Modes.
Introduces models which can have multiple modes

-> Single Gaussian이 아닐 때 multiple mode를 제약할 수 있는 constraint를 만들어 낸다.
Typical 가우시안 확률분포를 구하는 공식

이때 log를 이용하여 분포를 계산하게 되면 훨씬 간단하게 계산이 가능하다.
K개의 mode가 존재하는 경우

weighting term은 mode의 중요도에 따라 먼거리(outlier)라고 판단한 경우에는 적은 weight를 주어 중요도를 달리한다.
Sum of Gaussian을 사용할 경우에는 log 기법을 사용할 수 없어 간단화 할 수 없다는 것이 단점이다.
IDEA
확률분포의 근사값을 사용한다.
SUM operator를 MAX operator로 대체한다.

그래프를 보면 초록색 SUM operator일 때와 빨간색 MAX operator인 경우에 비슷한 경향의 그래프를 띠는 것을 확인할 수 있다.
또한 MODE끼리 서로 겹치는 부분이 큰 경우에는 정확도가 떨어지고, 겹치는 부분이 작은 경우에는 두 그래프가 서로 비슷한 것을 확인할 수 있다.

또한 MAX operation인 경우 log 함수를 적용할 수 있어, 식을 간단하게 처리할 수 있는 장점이 있다.
How to Intergrate
1. 모든 mode에 대한 Gaussian 확률분포를 계산한다.
2. 그중 가장 큰 값을 가지는 mode의 가우시안 확률분포를 선택한다.
3. 해당 가우시안 확률분포만을 가지고, optimization을 수행한다.(Single Gaussian 처럼 생각)

Result
Performance 측면에서 위쪽 performance를 볼 때 outlier가 많아질 수록 정확한 mapping이 이루어지지 않지만, 아래 Max Mixtures를 적용한 Perfomance를 보면, outlier가 많더라도 outlier가 적은 map과 거의 비슷한 map을 제작하는 것을 확인할 수 있다.
2. Dynamic Covariance Scaling.
요약하자면 outlier들과 같이 mapping에 별로 도움이 되지 않을 것 같은 error term에는 낮은 가중치를 두어 영향을 줄이는 방법이다.

빨간색 원으로 시그마 속에 둘러싸인 term이 error term이다.
이 경우 모든 term에 대해 같은 가중치를 가지기 때문에 무시하고 싶은 term이 있더라도 같은 영향을 주는 결과를 낳는다.
Dynamic Covariance Scaling

위에 보이는 수식 중 s term이 추가적인 scaling을 해줄 수 있는 term인데, error가 커질수록 scaling term이 작아져 estimation에 영향을 크게 주지 못하도록 제한하는 역할을 한다.
3. Least Squares with Robust Kernels.
Least Square 방법은 가우시안 분포에서 사용할 수 있는 방법이다.

가우시안 분포의 특성상 error가 커질수록 확률이 작아지는 모양을 띠고 있다.
하지만 Real-world에 존재하는 여러 outlier들이 모두 가우시안 분포를 띠고 있는 것은 아니기 때문에, 이들을 다룰 수 있는 분포의 모양을 구성하여야 한다.
Basic concept
Square error를 사용하는 것이 아닌 error value를 일단 가져오고, 사용자 지정 함수인 rho function에 대입하여 새로운 값을 얻어낸다.

rho function은 여러가지가 존재하는데, outlier의 종류에 따라 다른 rho function을 사용한다.


error가 일정 부분보다 더욱 커지게 되면 flat한 형태를 띠게 되는데, 이는 Jacobian이 0에 가까워지게 되고, 이는 error를 더 많이 무시할 수 있는 결과를 낳게 된다.
How to determine rho function?
Outlier가 어떤 분포를 가지고 있는지에 따라 달라진다!
outlier가 어떤 분포를 따르는지 계속 실험과 시행착오를 반복하면서 파악하여야 하고,
만약 Outlier가 Cauchy distribution을 따른다면 'Cauchy와 유사한 형태의 rho function'을 사용하여야 한다.
'그래픽스 > SLAM' 카테고리의 다른 글
| [SLAM] ORB-SLAM: a Versatile and AccurateMonocular SLAM System (0) | 2022.08.05 |
|---|---|
| [SLAM] Hierarchical Pose Graphs for SLAM (0) | 2022.07.31 |
| [SLAM] Graph-Based SLAM (0) | 2022.07.31 |
| [SLAM] Introduction to SLAM (0) | 2022.07.31 |




댓글